Discrete-time analogs of the exponential and logistic models

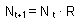
where t is time measured in generations, and R is net reproduction rate. For monovoltine organisms (1 generation per year), R is the average number of offsprings per one parent. For example, in monovoltine insects with a 1:1 sex ratio, R = Fecundity/2.

The dynamics of this model is similar to the continuous-time exponential model.

Logistic model analog (Ricker):

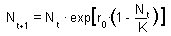
The dynamics of this model is similar to the continuous-time logistic model if population growth rate is small (0 < ro < 0.5). However, if the population growth rate is high, then the model may exhibit more complex dynamics: damping oscillations, cycles, or chaos (see Lecture 9). An example of damping oscillations is shown below:

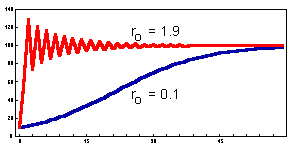
Complex dynamics results from a time delay in feed-back mechanisms. There are no intermediate steps between time t and time t+1. Thus, overcompensation may occur if the population grows or declines too fast passing the equilibrium point. In the continuous-time logistic model, there is no delay because the rate of population growth is updated continuously. Thus, the population density cannot pass the equilibrium point.