7.1. Model Structure
The model of Leslie (1945) describes 3 kinds of ecological processes:- Development (progress through the life cycle)
- Age-specific mortality
- Age-specific reproduction
- Nx,t = number of organisms in age x at time t (age is measured in the same units as time t). Usually, only females are considered and males are ignored because, as a rule, the number of males does not affect population growth.
- sx = survival of organisms in age interval from x to x+1.
- mx = average number of female offsprings produced by 1 female in age interval from x to x+1 (mortality of parent and/or offspring organisms is included)
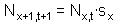 | [1] |
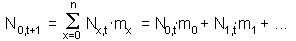 | [2] |
Equation [1] represents development and mortality, whereas equation [2] represents reproduction. Equation [2] specifies the number of individuals in the first age class and equation [1] specifies the number of individuals in all other age classes. In the equation [1], the number of individuals in age x+1 in time t+1 equals to the number of individuals in the previous age and previous time multiplied by age-specific survival rate sx. In the equation [2] the number of new-born organisms equals to the number of mothers (Nx,t) multiplied by the numbers of offspring produced (mx). The number of offsprings is summed over all ages of mothers.
These two equations can be combined into one matrix equation:
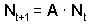
where Nx is the vector of age distribution in the population at time t, and A is the transition matrix.
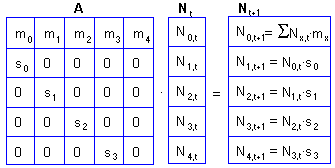
When a matrix is multiplied by a vector, we take the 1st row of the matrix, multiply each number by the corresponding number in the vector-column and then sum all products. This sum is the value of the 1st element in the result vector. Then we take the 2nd row of the matrix, multiply it by the same vector and the sum becomes the 2nd element in the result vector. In the same way we can estimate all elements of the result vector.
The first element of the result vector corresponds to the equation [2], and all other elements correspond to the equation [1].
How to read matrix models?
Each column specifies the fate of organisms in specific state. The number in the intersection of column i and row j indicates how many organisms in state j are produced by one organism in state i. In the Leslie model, organisms' state is defined by age only. For example, the third column corresponds to age a=2. An organism in age 2 produces m offsprings of age 0 (first cell in the column), and goes to age class 3 with probability s (the cell under main diagonal).
Most simple stochastic process is defined by a matrix of transition probabilities between states:
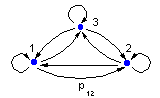
In this case, the sum of matrix elements in each column equals to 1 because it is assumed that each system passes through a series of states and neither die nor reproduce.
Leslie model is more complex because the sum of matrix elements in each column is not necessary equal to 1. This is a "branching process" because the life trajectory of a parent branches into life trajectories of its offsprings.
Matrix models are easy to iterate in time. In the next time step we again multiply the transition matrix by the vector of age distribution:
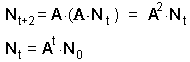
This equation can be used to simulate as many time steps as necessary.


