8.7. How to combine physiological time with the model of Leslie?
The model of Leslie can be easily modified to incorporate physiological time. In the original model age and time were equivalent because each time step organisms were moving to the next age class. Now age will be measured in units of physiological time! Each column and row in the matrix corresponds to a specific physiological age.
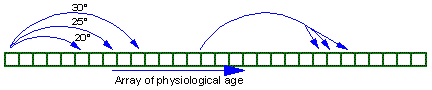
Progress in physiological age in one time step may depend on temperature (3 arrows at the left side of this graph).
Also, individual variation in development rate (distributed delays) can be taken into account (branching arrow at the right side of the graph).
At the start of simulation all organisms can be placed into the first age class. Another option is to add variability in the starting date of development. For example, if we simulate insect larval development, it is unrealistic to assume synchronous egg hatch in one day. It is better to assume distributed egg hatch time. Three kinds of distributions are used most often: normal, logistic, and Weibul.
Cumulative distributions are described by equations:
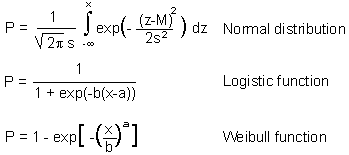
Two graphs below show how to convert cumulative probability function of egg hatch time into the proportion of eggs that hatch each day (logistic and Weibull distributions):
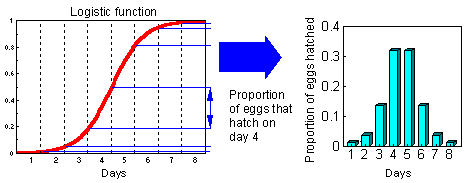
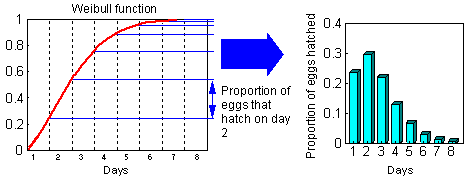
Normal and logistic distributions are both symmetrical and are very similar. But Weibull distribution is asymmetrical. Actual distribution of egg hatch time is often asymmetrical, and thus, the Weibul distribution is usually better than the normal and logistic distributions.