8.2. Simple degree-day model

In most cases, real development rate is indeed a linear function in the region of moderate temperatures (15-25°) (see figure above). Deviating points at temperatures that are too low or too high can be ignored. For example, in the figure, regression line is plotted for points from 10 to 30°. At 5° all organisms died and there was no development. At 35° organisms were overheated and development rate of survivors was reduced. If we are interested in simulating organism development in moderate temperatures, then the degree-day model will be the best choice.

Terms:

• t_min is the lower temperature limit; this is the temperature at which development rate reaches zero.
• ET = t - t_min is effective temperature.
• S are degree-days; this is the effective temperature multiplied by the number of days required to complete development.

where a is intercept, and b slope.

a + bt_min = 0, by the definition of the lower temperature limit. Thus,

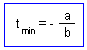
In our case, t_min = 0.0104 / 0.00142 = 7.3°.

Duration of development is T = 1/v. Thus, degree-days can be estimated as:

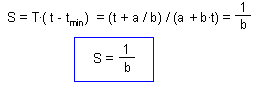
This equation shows that degree-days do not depend on temperature! This is the principal feature of the degree-day model. In our case, S = 1 / 0.00142 = 704 degree × day. The units of degree-days are degrees (centigrade) multiplied by days. Some times, it is better to use degree-hours if development is very fast.

Because degree-days are temperature-independent, it is possible to use them to predict development time in experiments with variable temperature. In this case effective temperatures are accumulated day by day, and when the sum reaches S, then development is finished.

Example: t_min = 10 , S = 100.

Day No.	Average Temperature t	Effective temperature, t - tmin	Accumulated degree-days
1	15	5	5
2	18	8	13
3	25	15	28
4	23	13	41
5	24	14	55
6	18	8	63
7	17	7	70
8	15	5	75
9	18	8	83
10	15	5	88
11	22	12	100
12	25	15	115

Accumulated degree-days reach the value S = 100 on day 11. Thus, it takes 11 days to complete the development.