Self-Reproducing Systems
Structure, Niche Relations and Evolution
Sharov, A.A. 1991. Self-reproducing systems: structure, niche relations and evolution. BioSystems, 25: 237-249. Get a reprint! (PDF)
- Summary
- Potential Self-Reproducing Systems
- Characteristics of Potential SRS
- Actual SRS
- Ecological Niches
- Evolution in SRS
- What is Missing in This Theory
Summary
A formal definition of self reproducing system is proposed using Petri nets. Potential self reproducing system is a subset of places in the Petri net and a subset of internal transitions (a transition is called internal if at least one of starting place and one of final place belong to the subset S) so that the number of tokens in all place in S increases due to firing of internal transitions with specific rates. An actual self-reproducing system is a system that compensates the outflow of its components by reproduction. In a suitable environment eny potential self-reproducing system becomes an actual one. A Petri net can be considered as an "ecosystem" with ecological niches in it.Potential Self-Reproducing Systems
All living systems are self-reproducing. Thus, if we want to understand what is life, we need a definition of self-reproduction. This document is a summary of my paper: Sharov, A.A. 1991. Self-reproducing systems: structure, niche relations and evolution. BioSystems, 25: 237-249. However, some definitions are modified here to make it easier to understand.Self-reproduction can be formulated using Petri-net models. Petri net were designed to represent dynamical systems in which individual objects can change their state, interact with other objects, produce new objects, etc. Formally, Petri nets have two types of components: places (=positions) and transitions. A place is interpreted as a class of identical objects or as a state of an object. Transitions are interpreted as processes that either change the state of objects or describe interactions among objects.
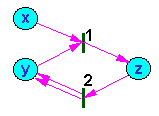
Fig. 1. Example of a Petri net; x, y, z are places; 1, 2 are transitions
Transitions are connected with places by arrows (Fig. 1). If an arrow goes from the place to the transition, then the place is called a starting place for this transition. If an arrow goes from the transition to the place, then the place is called a ending place for this transition.
Each place is characterized by the number of tokens in it. A token is interpreted as a member of class represented by the place. For example, the change of object state (e.g., development of an organism) is equivalent to the transfer of a token (organism) from one place (initial stage) to another place (final stage). The number of tokens in all places is called marking of the net. Each marking can be viewed as a vector in a multidimensional space. Each dimension corresponds to a place and the projection of the vector equals the number of tokens in this place.
It is assumed that transitions in Petri nets are executed (=fired) instantly. This assumption works well in automated contol systems which is the major area of application of Petri nets. However, in biological systems, some changes are gradual, e.g., growth or development. When we approximate a gradual change by transitions we need to subdivide it into several portions which become links in a chain of transitions. We will also assume that any transition in the net is an elementary change and cannot be represented as a superposition of two other transitions.
The rate of processes is not defined within a Petri net, it should be specified separately. In automated control systems represented by Petri nets, execution of transitions usually depends on the presence of specific number of tokens in all staring places. However, in most chemical and biological systems the rate of processes (transitions) is defined by the mass action law: it is proportional to the product of the number (or density) of tokens in all starting places as shown in the figure below.
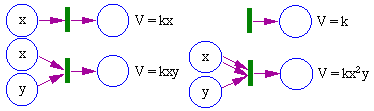
Fig. 2. Mass action law; V is the rate of firing of the transition; k is the constant; x, y are the numbers (or concentration) of tokens in starting places.
The mass action law is used in many models of population ecology (exponential growth, Lotka-Volterra eqns.). Some processes may involve a delay in interaction (Michaelis-Menten eqn., Holling’s model of predation). As a result, the mass action law becomes violated.
Now we will introduce the definition of a potential self-reproducing system (SRS). We will approach the definition in several steps.
- SRS cannot be defined as a single plase because self-reproduction requires a life-cycle which is a trajectory that goes through several places (=stages of development). Thus, an SRS includes a set of places, S.
- A SRS also includes a set of transitions (processes) that are essential for selfreproduction: development, growth, mating, and reproduction. All these transitions have at least one starting place and at least one final place in the set S. This kind of transitions we will call internal to the set S. Internal transitions always connect places within S.
- Places in S may be involved in external (=non-internal) transitions. Examnples are: mortality, emigration, and immigration.
- The marking of the SRS is the vector V with projections equal to the number of tokens in each palce in the subset S. For example, population age structure is often represented by a vector with elements equal to the number of organisms in each age class. Age class is a place and the number of tokens is the number of organisms in this age class. Another example is a sexual structure which is a vector in a 2-dimensional space with male/female coordinates.
- When a transition is fired, then the marking of the SRS changes because some tokens are taken from their places and some tokens are added to places. The difference between the final and initial marking vectors is the vector of marking change, v(t,S), where t is a transition, and S is a subset of places.
- Now we can define a potential SRS as a set of places S, if positive weights w(t) can be assigned to internal transitions, t, so that all projections of the sum
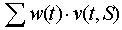
[1] are positive. This means that if internal transitions are fired with the rate proportional to weights w(t), then the number of tokens increases in each place of the set S.
Fig.2 shows another example of potential SRS that represents a population with sexual reproduction. The upper cycle corresponds to females and the lower to males. Fertilized females (1) produce female (2) and male (3) progeny. Progeny assimilate some resources (4) and mate after completing their development. The potential SRS that corresponds to the entire population (places 1, 2, 3, 5, and 6) has two smaller potential SRS inside: the male SRS (places 1, 2, and 5) and the female SRS (places 1, 3, and 6). Males use females as resources for their self-reproduction, and at the same time females use males as resources for their self-reproduction.
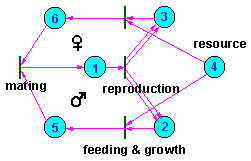
Fig. 3. Petri net representing a population with sexual reproduction
Characteristics of potential SRS
- Each potential SRS has at least one internal transition, the execution of which increases
- the number of tokens in the system.
- If the law of conservation of mass is true for any internal transition t of some potential SRS then there is at least one resource. When a potential SRS increases the number of tokens, then "mass" is increased. This may happen only if there is a resource for mass increment. Examples of resources: place x in Fig. 1 and place 4 in Fig. 2.
- A minimal potential SRS is a cycle.
The potential SRS, S, is called minimal if it does not contain another SRS inside. For eaxmple, the bisexual population in Fig. 2. is not a minimal SRS because it has 2 smaller potential SRS inside (males and females). A cycle is a set of places S, where any place can be reached from any other place through a sequence of transitions that connect places within S. The proof that a minimal potential SRS is a cycle can be found in Sharov (1991).
Actual SRS
Potential SRS is a system that can reproduce itself if transtions are fired at specific rates. In real systems, the rate of transition firing depends on the numbers of objects (tokens) in each place. The numbers of objects change with time and this may change the rate of transition firing. We assume that the dynamics of the system approaches some sort of asymptotic behavior: (1) steady state, (2) limit cycle, or (3) chaos.If we take a subset of places S, and a subset of its internal transitions T, then we can test if the number of tokens in the subset S is supported by transitions in T. Let w(t) be the average rate of firing of transition t. The subset of places S is the actual SRS if all projections of the sum [1] are positive. Self-reproduction in the actual SRS is balanced by mortality and thus, in average, there is no change in the number of tokens. Actual SRS can be partially supported by immigration.
It is obvious that any actual SRS is a potential SRS. In a suitable environment, any potential SRS may become an actual SRS (Sharov 1991). For example, if all resources are available in a sufficient quantity and natural enemies are absent, then the SRS can reproduce itself.
Ecological Niches
Petri nets can represent ecological systems with multispecies communities. Species can be considered as a unit in the ecological community. Being a unit means that (1) portions of a species cannot exist separately; a species can be either present in the community or absent but nothing intermediate; and (2) no species can originate from another species in the ecological time scale. For example, males and females of the same species are irreplaceble resources for each other. It is impossible for a community to have only males or only females (unless females are parthenogenic). If a species has facultative parthenogenesis (e.g. at cold temperature) then females can live without males. However, males will eventually originate from females at specific conditions, and thus, males cannot be considered as an independent species. This is an ecological definition of a species which does not consider any evolutionary criteria.One of the problems with the definition of a species is intra-specific polymorphism associated with different biotic resources. For example, aphids feeding on different plant species may differ in their color, size, fecundity, and other characteristics. Let's assume that there are two forms of aphids of the same species feeding on 2 host plant species: A and B. If only plant A is present in the ecosystem, then all aphids will be found on plant A and will have morphological characteristics specific to this host plant. If we introduce plant B, then another form of aphids will appear immediately. Here, aphids have two "ecological niches" which correspond to the same species.
Now we will formalize the definition of ecological niche and species using Petri nets. The idea of this formalism is the following. Ecological system represented by a Petri net can exist in several stable states with some niches occupied and some niches non-occupied.
For example, a hypothetical ecosystem with 2 producers (A and B) and 2 consumers (C feeds on A, and D feeds both on A and B and these resources are replaceble) can have the following combinations of niches (in this example we assume that all species have unique niches and thus we don't need to distinguish between them):
| 1. Niches empty | 5. A+C | 9. A+B+D |
| 2. A | 6. A+D | 10. A+B+C+D |
| 3. B | 7. B+D | 11. A+C+D |
| 4. A+B | 8. A+B+C |
Forbidden combinations are:
| 1. C | 3. C+D | 5. C+B+D |
| 2. D | 4. C+B |
Each allowed combination of niches will be called an autonomous set (definitions will be given below, here it is just an explanation). A niche is a difference between two non-equal autonomous sets Q1 and Q2, one of which includes the other (Q1
This figure shows the Petri net with autonnomous subsets. The smallest autonomous subset is Q1={p1,p2}. It does not include any selfreproduction and can be interpreted as the "abiotic" component of the ecosystem. If only places p1 and p2 are filled with tokens, then all other places remain empty.
If a token (an organism) appears in place p3, then it will be able to reproduce using p1 as resources. Then the ecosystem will increase to the autonomous subset Q2={p1,p2,p3,p4,p5}. Places p3 and p4 represent the life cycle of the first "species" which can be classified as a producer because it uses only abiotic resources. Place p5 is not involved in self-reproduction and can be interpreted as carcas which "decomposes" and turns into component p2.
The next autonomous subset Q3={p1,p2,p5,p6,p7} includes the second
"species" {p6,p7} (which is a producer too), "carcases" = p5, and non-living components p1 and p2. Another autonomous subset Q4={p1,p2,p3,p4,p5,p6,p7} includes both producer species. The next autonomous subset Q5={p1,p2,p5,p6,p7,p8,p9} includes the previous subset plus a new "consumer" species {p8,p9} which uses biotic resource, p6. Finally, the largest autonomous subset, Q6, includes all places in this Petri net. It includes all 3 species: 2 producers and 1 consumer.
It is clear from Fig. 4 that the difference between autonomous subsets may be larger than a niche. For example, the difference of subsets Q2 and Q1 (Q2\Q1 = {q1,q2,q3,q4,q5}) includes carcases, q5. The place p5 is different from other places in Q2/Q1 because there is no internal transition going from p5 to other places in Q2/Q1. As a result, q5 is a terminal state from where there is no way back to normal "organisms" of the niche {q3,q4}.
Thus, I defined a niche as a set of places S that:
Basicly, a species is a set of intersecting niches. Each niche can be filled from any other niche of the same species is corresponding resources are present in the environment. Let's return to our example with an aphid species that may feed on 2 host plants. It is important, that the population of aphids on one host plant may go to another plant when it becomes available. These transitions should be simmetrical: if aphids can go from plant A to plant B, then they should be able to go back from plant B to plant A. If transitions between niches are not symmetrical (they work only one way), then the combination of these two niches is not a species.
Theoretically I can imagine niches which do not correspond to any species, and the notion of species becomes useless. It seems that this happens in the evolutionary time scale, where changes become irreversable. The concept of species is probably of little use in the evolutionary scale. However, I don't want to go further because this topic is not enough clear to me.
Let's consider the stationary dynamics of some Petri net. Some niches are filled in this dynamics, some are empty. A niche will be called closed if it cannot be invaded, and a niche that can be invaded will be called open.
Invasion can occur due to immigration of mutation of existing organisms
ESS is - "a strategy such that, if all the members of a population adopt it, then no mutant strategy could invade the population under the influence of natural selection" (Maynard Smith 1982, p.10). This approach can be adopted for Petri nets: a stationary dynamics of the Petri net is evolutionary stable if it is not sensitive to the introduction of small number of any kind of objects. This means that there are no open niches.
When environment changes, some niches may become open. As a result, a cascade of evolutionary changes may start until the process ends in the next ESS state.
There is no big problem to define topology in Petri nets and assume that transitions keep this topology. However the theory will become very complex and it is better to leave it to mathematicians.
Another missing feature is "information". I did not consider any program (genetic information) that controls transitions. Thus, my approach is different from the approachg of Von Neumann who considered programs and programmmable constructors.
I think that information is closely related to topological problems. Information process is always an amplification of a small signal into large changes. This happens through the instability of system trajectory, when the small informational input can affect selection of future trajectories (see my paper on biosemiotics)
(a) all terminate places of each active transition in S belong to S; and
(b) there are rates w(t) for active transitions t, which increase the number of tokens in each place of S.
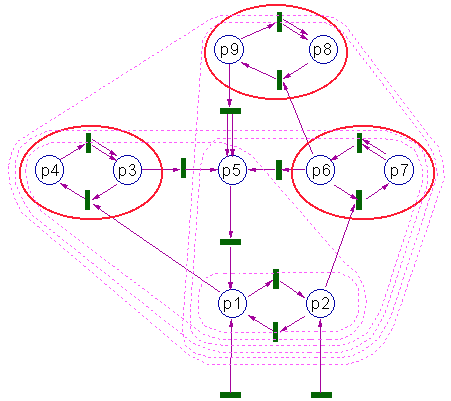
Fig. 4. "Ecosystem" represented by a Petri net. Autonomous subsets are encircled with magenta dashed line. Niches (species) are ebcircled with red solid ellipses
It is easy to check that all three niches in Fig. 4 satisfy this definition.
In my paper (Sharov 1991) I have proved that
Now we can return to the notion of species. At this point I don't have a satisfactory definition of a species. Thus, I will only explain how I view the development of this definition.Evolution in SRS
No single model is able to cover all topics in the evolutionary theory. Thus, I don't expect that Petri nets will be useful for any kind of evolutionary problems. However, they may be helpful in some areas of the evolutionary theory, e.g., for models of evolutionary stable strategies (ESS).What is Missing in This Theory
The major missing thing in this theory is a kind of topology which would specify places that are "close" to each other and places that are "far" from each other. Darwinian evolution is a topological phenomenon because it assumes small mutations and continuous change of fitness. If fitness was discontinuous, then the offspring of successful parents will not be successful. Peter Munz use the term "regularities" to specify the continuity of fitness.
Alexei Sharov 04/22/96