
Yuli (Julius) Schreider
On Systems and Models

| Yuli (Julius) SchreiderOn Systems and Models
|
| Element/Whole
| Wholes can be partitioned into components
| Elements can be combined into a set
| Relations among components
| Components are either similar (correlated) of interconnected
| Elements in a set may be unrelated (e.g., a set of star, apple, and freedom)
| Individuation of systems
| Individuals (systems, components) emerge in the process of interaction with the observer. Components can be identified only from a comparison of various systems (as biologists do). Systems are often fuzzy (we are not sure whether some component belongs to the system).
| Individuals are defined a priori. Thus, comparison of systems is observer-independent (extensionality principle). For example, 2 sets are equal if they have the same elements. An element either belongs to a set or does not belong (no fuzziness).
| Internal/External organization
| Systems develop their organization internally. Partitioning of the system is a result of its internal development. Metaphors: self-organization, development of an organism, directed evolution.
| Sets are constructed externally (by a human, or by chance). Metaphors: assembling a mechanical watch; natural selection.
| Probabilities vs. individuality.
| Systems that have internal integrity often have a limited number of components. Although relative abundance of components represents the individuality of a system and can not be studied using probabilities.
| Theory of probability is based on the assumption of large sample sizes. Because sets may have an unlimited number of elements, they are used as a foundation of the probability theory.
| |
2. Two kinds of systems: internal and externalInternal system1) is an integrated whole that can be partitioned in several ways and represented as a set of components connected by relations. Each representation is a structure (or archetype) of the system. Schreider also believed that besides archetypes-representations there is a unique archetype-essence.2)
Examples: a living organism, ecosystem, solar system, atom, galaxy. Examples: biological taxons: species, orders, types; chemical elements (oxygen, nitrogen). Both kinds of systems are characterized by harmony that may be manifested in a symmetry, rhythm, or style. Both systems are not sets but can be represented by sets. Internal systems may have fuzzy components; some objects may correspond to an archetype of an external system only partially. A representation of a system is a model, and there are relationships (morphisms) among various representations of the same system.
3. Complex systems and ControlComplex systems must have a large number of components, but the large number of components does not mean that the systems is complex. A complex system should also have high organization. High organization can be recognized by multiple hierarchical levels, efficient functions, and ability to learn.
In simple systems, information is processed at a syntax level. Simple systems may include complex systems as components. For example, a military unit is simple system because it interprets commands literally, but each person is a complex system. An example of syntactic control is developing a hierarchy of goals from the highest-level goal. Semantic control required developing a system of common values rather than goals. In syntactic control, a sub-system does not care about higher-level goals. Semantic system of control has a fuzzy hierarchical structure because elements of one level may also represent higher-level values.
4. Models and TheoriesModel is an abstract system that represents some aspect of a real system. The same system may have different representations (models).A model is a set of elements, S, with some relations, {Ri}, defined on this set. All relations are named using vocabulary N. Models are equivalent if their relations are named using the same vocabulary N, and there is an isomorphism (reversible function) between their sets that conserves all their relations. A theory is a formal language that specifies the characteristics of relationships. For example, the group theory has 2 relations: a binary operation: a + b = c, and a special unity element I. These relationships are characterized by 5 axioms:
A model, M, satisfies theory T if they correspond to the same set of names for relations, N, and each axiom of T is true in model M. For example, a set of integer numbers with the sum operation and zero as a unity element satisfies the theory of groups.4) The most interesting thing is that in many cases we can describe all possible varieties of models that correspond to a specific theory. The number of non-equivalent models that correspond to the theory may be limited. In this case we get a natural class of models that correspond to some theory. For example there is a limited number of continuous topological spaces of a given dimension. Theories can be viewed as platonic ideas that have no substance (no material set). They have meaning only within a particular language practice. For example, Stanislaw Lem wrote in "Star diaries of Ion Tichy" about some planet on which inhabitants used an object called "sepoulka". Ion Tichy tried to talk to several creatures on this planet trying to understand what is "sepoulka" but did not succeed because he had no chance even to see how this object looks like. What he got from answers was a formal theory without reference to a specific set. Real objects also can be viewed as models of some formal theory.5) For example, the solar system is a model of the theory of gravity. A computer model of a solar system is a model of the same theory. But the ontological status of these models is different because they are embodied in different sets. But a model is just one representation of the system among many other possible representations because formal descriptions of systems are always incomplete. A theory T is called consistent with the class of models K if any model from K corresponds to the theory T. A theory T is complete for the class K if for any model of theory T we can find an isomorphic model in K. In natural sciences, it is a rare case if the theory is both consistent and complete. Usually it is consistent with the majority of models or almost consistent with all models. For example, a theory of mammals may include an axiom that mammals don't lay eggs. However there are a few mammal species that lay eggs (e.g., a duckbill). Schreider also defined frames as something intermediate between a model and a theory. A frame has a set (as a model) and some of relations between elements. But there are some additional relations that have not been defined yet which should satisfy specific axioms. For example, a fabric can be considered as a frame on which we can put additional color patterns.6) Then a system can be represented as a class of frames (possible representations) with morphisms between these frames. If the state of one frame changes, the state of other frames may change respectively according to morphisms.
5. Taxonomy and MeronomyTaxonomy is the method for grouping objects into natural classes which often have a hierarchical structure. Meronomy (a term was introduced by Sergei Meyen) is the method for partitioning internal systems and classifying parts ("meros" = part in Greek). Objects in one natural class are characterized by the same theory and usually correspond to a specific term in the human language. A taxonomy is called natural if it allows to predict essential characteristics of objects from the fact that they belong to a specific taxon.7) Natural classes of whole systems is a taxon, and a class of parts of systems (these parts may belong to various systems or to the same system) is called a meron.Biologists claim that natural classification of organisms should always correspond to the phylogenetic tree. Schreider argues with this view: (1) phylogeny is often reconstructed from the analysis of morphology, (2) classifications in other sciences, e.g., in chemistry, are not phylogenetic, and (3) it is possible that organisms on other planets (if they exist) are similar to organisms on the Earth and can be classified together despite the fact that they have no common ancestors.8) Classification groups individuals from a classification universum into taxons. Classification universum is a class with fuzzy boundaries. Generally, it is not clearly defined what is a single organism (e.g., a single stem of a bamboo or the cluster of stems). A species can be defined as a minimal taxon. Then, a higher taxon can be viewed as a subclass of species. Classifications can be hierarchical, combinatorial, and mixed. The class of species can be a regular set, if species are well separated (no fuzziness). But in many cases, species are not well separated. For example, taxonomists often disagree on the status of species and subspecies. Some of them rise subspecies to a species rank. If we classify buildings by their style, then again we will not find clear "species" of style. The relationship between taxonomy and meronomy is that each taxon can be characterized by some archetype that is true for all individuals (or species) that belong to this taxon. This assumption is equivalent to the existence of a concept for each notion in the language. Schreider considers an archetype as a frame (see above) built on the set of merons. Homology between parts of systems is the consequence of sharing the same archetype. Each part of a system corresponds to some meron in the archetype. Parts in different systems that correspond to the same meron in the archetype are homologous. Each meron may have different states. For example, legs may be more developed in some species and less developed in other species. Also legs may be for running (deer), digging (mole), jumping (kangaroo), swimming (seal), and flying (bats). These are states of the same meron. Merons may have a zero-state, like legs in the snake. Both taxons and archetypes have a partial order. Taxons are ordered by inclusion. For example, the taxon of chimps is included in the taxon of primates. Archetype A is greater than archetype B (A > B) if all merons and relations between them in B are present in A. If B has axioms, then all additional merons in A satisfy these axioms. In terms of category theory, there is a monomorphism from B to A. Orders in taxons and archetypes are opposite which was called a duality principle of classification:
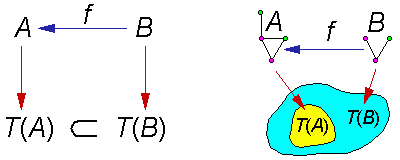 Duality principle of classification. Smaller archetype (B) corresponds to a larger taxon T(B). Using the terminology of the category theory, T is a contravariant functor to the category of classes. For each archetype it indicates its taxon which is a class. Because an archetype is a formal theory of objects that belong to the taxon, they may be used to predict potential variability of members of this taxon. For example, the periodic table of chemical elements predicts potential variability of each group of elements. This method may work even in biology. For example, Nikolai Vavilov (1992, Origin and geography of cultivated plants) built a periodic system of varieties of cultivated plants. Sergei Meyen (1987) built a combinatorial system of leaf segmentation:
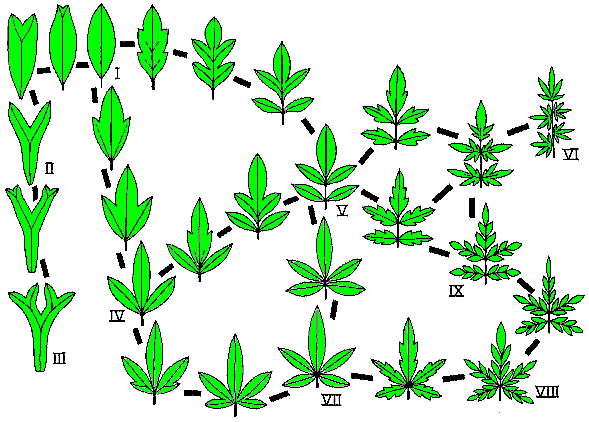 Scheme of leaf segmentation. Pattern VI is a combination of patterns V and VII; pattern III is an iteration of pattern II. (from Meyen, S.V. 1987. Fundamentals of paleobotany).
6. Voting systemsVoting systems can be classified into symmetric and asymmetric. In a symmetric voting system, voting rules do not depend on the proposed item. For example, if some set of people voted for A and A was selected, then if the same people had voted for another item B, then item B is selected. In an asymmetric voting, rules depend on the subject of voting. For example, the opinion of experts may be weighted more if the subject of voting is in their area of expertise. But because people are experts in different areas, voting rules will depend on the subject of voting. Schreider studied both kinds of voting systems. He developed a model of coalitions for asymmetric voting and the model of majority structures for symmetric voting.Let us assume that the set of people, X, votes for one of 2 alternatives: A or B. It is assumed that all people from X participated in voting, each selected only 1 option (A or B), and all ballots were valid. Then axioms of the coalitions are:
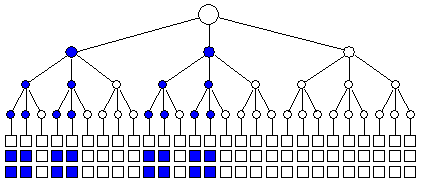 Squares are voters; they are colored blue if they vote for A, and white if they vote against A. Circles are hierarchical groups of voters that make a decision sequentially according to the majority of elements within a group. Circles are colored blue if the group selects A, and white if it does not select A. The whole system selects A although only 16 people out of 81 voted for A. As the total number of voters increases to infinity (and voters have equal rights), the proportion of voters in the smallest coalition may approach zero. However, the number of people in the smallest coalition is always greater than the square root of the total number of voters. This model of majority voting can be applied to the problem of identification of systems. Each characteristic can be viewed as a voter, and the decision is to accept or reject the hypothesis that the system corresponds to the archetype. Even if all characteristics are equally important, the decisive role may belong to a relatively small coalition of characteristics. Thus, a system may belong to a taxon even if it has a small number of characteristics that correspond to the archetype.
Semantic informationShannon's theory of information defines the quantity of information, but it does not say anything about how it is interpreted by a person who receives this information. May be the interpreter already knows this information and thus, the message is simply redundant and can be ignored. To characterize the meaning of information it is necessary to know how this information changes the knowledge of the interpreter.The first step is to define what is knowledge. Knowledge can be viewed as a generalized taxonomy, i.e., as a set of names for taxons and merons which are associated with corresponding archetypes. Because parts of archetypes (merons) belong to the same generalized taxonomy, archetypes define relations between names of taxons and merons. For example, the word "leg" is associated with animals and furniture (table legs), and word "tax" is associated with "IRS". Knowledge A can be considered greater than knowledge B if it contains all archetypes from B with possibly added complexity and have some additional archetypes. When a person receives a message, his knowledge usually increases. Let us assume that we managed to measure the amount of knowledge in some relatively narrow area. Then the increment of knowledge after receiving a message can be plotted against the amount of initial knowledge:
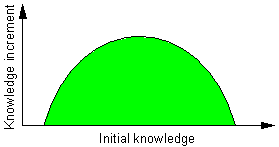 The initial of knowledge affects the amount of information that can be extracted from a text (knowledge increment). Small initial knowledge is insufficient to understand the message and the increment of knowledge is small. As initial knowledge increases, the interpreter understands the message in more details and the increment of knowledge grows. But at some point, the interpreter finds that he already knows some information in the message. After that the increment of knowledge decreases and eventually reaches zero at the point where the interpreter does not find anything new in the message. Of course, this figure is an oversimplification because two knowledges may be quantitatively equal but essentially different qualitatively even if they are limited to a specific area. But nevertheless, this figure captures some important characteristics of information processing. First, knowledge can not grow without preliminary knowledge. Second, redundant information does not increase knowledge. If initial knowledge is insufficient, then the text is understood only syntactically. For example, when we read a book in a foreign language which we don't know very well, we understand the structure of sentences and most of the words. But we get only a vague idea of its contents. Computer programs are able to understand the syntax of computer code but they do not understand the purpose of this code. The next level of understanding captures literal semantics. At this level it is possible to understand technical texts, e.g., scientific papers, but it is impossible to understand jokes or parables. The next level of understanding is deep semantics include jokes, the purpose and main idea of the text, philosophical background of the author. Finally, there may be a dialog with a text, e.g., if you return to this text many times and always find something new. In this case, understanding is not a state but a process. The question is why information can not be understood without some preliminary information? Schreider suggests that in order to understand some information we need to know how it is structured. Thus, preliminary information can be called metainformation because it is information about information. This idea is closely related to the idea of metalanguages suggested by Tarski. Regular information is what we call "facts", but metainformation is the knowledge about how these facts are organized. In other words, metainformation is the theory of knowledge, i.e., methodology. Language is the carrier of semantics, and the depth of semantics depends of the structure of the language. Schreider considers 3 kinds of languages:
Goals and valuesDo we follow goals in our behavior? It appears that goals are not used as often as we may think. A goal-oriented behavior means that we optimize our actions in order to reach a specific event at a minimum cost. For example, if we want to buy a new TV, we first save some money, then go shopping and check prices, and finally our goal is reached: we got a TV. Goal-oriented behavior always have a time limit. After we bought a TV, we will do something different.Instead of setting goals, humans are more often follow some rules of rituals in their behavior that are not oriented to some final event for the sake of which they are done. For example, if we save money we often have very vague ideas about what we are going to do with this money (e.g., after retirement). If we watch TV we may find it generally entertaining and may be useful, but we never watch TV for the sake of some higher goal. People rarely make love just because they want a baby. Usually love has a value on its own. Goals are often seen in systems that have no goals. For example, among all possible trajectories from point A to point B light always goes by the one that requires minimum time. For example, if the speed of light in glass is slower than in the air, then light refracts as shown in this figure:
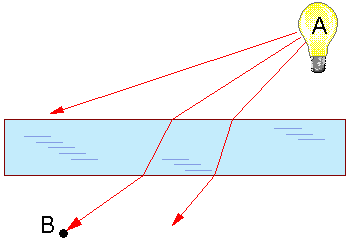 Among all possible trajectories from point A to point B light always selects the fastest one. This can be interpreted as if light has a goal to get to the point B as fast as possible. However, this is not a goal because:
Goal-directed behavior is a good model for a criminal investigation. For example, punishment depends on whether the murder was intentional or incidental. It is sufficient for the court to know that the murder was intentional (i.e., goal-directed behavior), and it does not matter why the person had that goal. If we want to understand a person deeper, we have to go beyond goals. Each goal requires an explanation why this specific event became a goal. And the only explanation for a goal is a system of values. If a person is consistent in selection of his goals this may indicate the presence of a specific system of values. Goals are external for the system but values are internal. Results of goal-directed behavior may have some value even if the goal was not reached. For example, if we learn by tries and errors, an error is usually not an ultimate failure but a part of a learning process. The proof of the impossibility to reach some goal may be very important for planning future activities. In value-directed behavior, there is no dominance of the higher-level element over lower-level elements (goal justifies the means), but instead, all elements of the hierarchy have some value. In goal-directed behavior, the freedom is limited by the goal. The system may select means to reach the goal, but the goal can not be changed. In value-oriented behavior, goals can be selected according to values, and thus the person have more freedom.
Comments1. Internal and external systems can be interpreted as systems pointed by two kinds of signs: indexes and icons (Peirce). Internal systems are pointed by indexes, and external systems are pointed by icons (archetypes). An icon points to a class of systems rather than to an individual system. The notion of a class was invented by mathematicians to escape paradoxes of the set theory; thus, a class is always considered as something like a set but not exactly a set. This interpretation assumes that a class is a multiplicity of objects. However, if a class is a multiplicity, then it contains indexes to individuals, and hence it becomes a mixture of both kinds of signs (icons and indexes). I suggest interpreting a class as a pure icon (archetype) that does not have any explicit multiplicity. However, to build an archetype we need to compare several representatives that (we believe) belong to the class. If human knowledge increases we may need to change our classification of objects in the world. To follow the evolution of archetypes it is important to keep several representatives of a class (a set of indexes). Biologists use holotypes for this purpose.2. Existence of an archetype-essence implies the existence of a super-observer (God) who grasps the essence of things (Schreider was a Catholic). Apparently, the existence of archetype-essence was needed as a basis for natural classifications and for normative ethics. My personal view is that we don't need neither natural classifications nor unified normative ethics. I believe that various classifications and various ethical systems compete for human minds. Different ethical systems may coexist by finding niches in different human communities. This view is well elaborated by Matt Nuenke in his paper The immorality of morals and the future of amorality. 3. The difference between models and theories is not absolute. We may reserve a set of names for individual elements of the set in the model. These names can be viewed as unary relationships. Thus, we can interpret models as theories of the lowest level. Then we develop mere general theories (higher levels) that can be represented by multiple models. The hierarchy of theories can be defined as follows: theory T2 is more specific than theory T1 (T2 > T1) if their relationships have same names, N, and if any axiom of theory T1 can be derived from axioms of theory T2. Then models can be defined as most specific theories. In the case of infinite sets, most specific theories may have an infinite number of axioms which does not fit to our intuitive notion of a theory or proof (Goedel's theorem). But models with infinite number of elements are equally contraintuitive because it is impossible to observe all its elements. 4. If the model has an infinite number of elements it may take infinite time (or infinite computer) to test that it satisfies the theory. 5. This statement seems to ignore the importance of measurement. I prefer to say that records of system measuring (e.g., observations of planets in the solar system) may appear to be a model of some theory. 6. I believe that the notion of a frame is redundant because models can be viewed as most specific theories (see comment 3). Thus, a frame is just a theory at some intermediate level of hierarchy. 7. Multiplicity of representations of the same object implies that there may be several classifications for the same group of objects. Schreider claims that there is some optimization principle according to which some classifications are better (more "natural") than others. I would argue that the quality of a classification depends on the way it is used for practical purposes. Thus, some classifications are more "natural" for one group of users whereas other classifications are more "natural" for other users. There is no classification that equally satisfies everyone. If there is a need to have one classification as a standard for everybody, then voting could be a good way to decide which classification to select. But I would not call it "natural". 8. Molecular biology has accurate methods for estimating phylogenetic relationships without considering morphological characteristics. I believe, there is no need to argue which system is more "natural". Apparently, both systems based on morphology and phylogeny are useful. Because they largely coincide, there is no sufficient reason to oppose one of them to another (except a few cases). Thus, I don't mind to use the phylogenetic system, although I agree with Schreider that a good classification can be built solely based on morphology (as it has been traditionally done for centuries). 9. Schreider use the term language in a broad sense as any system of signs. I prefer to reserve the term 'language' only for hierarchically structured systems of signs. However, there is no generally accepted term for non-hierarchical systems of signs. I suggest to use the neutral term 'semantic repertoire' for any kind of sign systems, including languages.
|
 Biosemiotics Homepage
Biosemiotics HomepageAlexei Sharov 11/02/1998