Lab 3. Sequential sampling plan for the gypsy moth

2. Open the file from the Microsoft Excel. This file contains data on sampling gypsy moth egg masses in West Virginia, near Morgantown. X and Y are longitude and latitude UTM-coordinates (Universal Transversal Mercator), zone 17, are measured in meters. E is the number of egg masses found in a 0.01-ha sampling plot. Data was taken from a rectangle area of 4 x 20 km.

Sampling methods. Each plot was a circle with the radius of 5.6 m. All new gypsy moth egg masses encountered within a circle were counted. Egg masses located within taller portions of a tree were counted using binoculars. New egg masses can be distinguished from old egg masses by their color and texture. Old egg masses are soft and have a gray/white color whereas new egg masses are hard and have a brown color to them. If both old and new egg masses were present in the plot, then the proportion of new egg masses was calculated from egg masses that can be reached from the ground. Egg masses located in the crown of the trees cannot be visually separated into new and old. Thus, the total number of egg masses was counted and then multiplied by the proportion of new egg masses.

3. Plot the location of traps. Subdivide the area into 2 x 2 km blocks (note: use FLOOR function to convert real numbers to integers). In each block estimate the average population density, SD, SE, and confidence intervals. Compare average population densities in different blocks. Show significance of differences using ANOVA. According to the Fisher's method, the difference between 2 means is significant if it is greater than

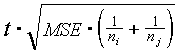
where t is the critical t-value of Student's distribution (usually, t=2), MSE is the mean squared error (take it from ANOVA), and ni and nj are sample sizes.

Use log-transformation (log(N+1)) to make uniform variances. Compare ANOVA results before and after log-transformation. Did the log-transformation improve the analysis?

4. Predict defoliation in the next year in these 20 blocks. Use the model of Gansner et al. (1985, North. J. Appl. For. 2: 78-79):

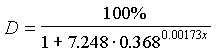
5. Estimate aggregation indexes: CD and mean crowding for 20 blocks.

6. Estimate density-invariant characteristics of spatial distribution: Taylor's power law, and the mean crowding regression. What can you tell about the spatial distribution of egg masses?

7. Develop a sequential sampling plan to reach the accuracy of 10, 20, and 30%. 8. Develop a sequential sampling plan to determine which areas to spray by pesticides in order to prevent defoliation. Use the following parameters:
Low population threshold = 1200 egg masses per hectare
High population density = 3500 egg masses per hectare
Alpha (risk of not spraying a high population) = 0.05
Beta (risk of spraying a low population) = 0.1
Estimate parameter k using the method of moments from field data. Use only those blocks where the average density was > 1000 egg masses per hectare. Estimate the average k-value for these blocks.

9. Write a lab report using the Microsoft Word. Optional: Convert your report into the HTML language. Incorporate cross-references to gypsy moth WWW-sites, pictures, etc.

Use this checklist to improve your lab reports!