Lab 4. Statistical analysis of population dynamics
The objective is to develop a model that can predict outbreaks of gypsy moth in north-eastern states of the US: Maine, Massachusetts, Vermont, New Hampshire, Connecticut, and New York. North-eastern states were selected because records of areas defoliated by the gypsy moth are available starting from 1927, except the New York state, where first defoliation was recorded in 1944. Dynamics of defoliation is probably related to the dynamics of population numbers area-wide. Thus our analysis can be used for understanding gypsy moth population dynamics. We will use defoliation areas in years t-1 and t-2 as predictors of defoliation area in year t. Also we will try to use temperature data to improve the prediction.1. Save files "gmdefol.txt" and "weather.txt" in the student's folder or any other temporary folder. Open these files from Microsoft Excel.
Data.
Area defoliated is measured in acres. Defoliation was recorded by the USDA Forest Service using aerial sketch maps and was generally detected at a threshold of 30% foliage loss.
Monthly temperature data was retrieved from the National Climatic Data Center (Global Historical Climatology Network), URL-address: http://www.ncdc.noaa.gov/ghcn/ghcn.html. We selected 32 weather stations with most complete data in the following area: latitude 42.8-44.9, longitude 68-74 degrees. Average temperature for each month was estimated using the GLM procedure (MINITAB). Year, latitude, and elevation were used as predictors (latitude and elevation were covariates). The GLM generated averages adjusted to the average elevation (210 m) and average latitude (44.06 degrees).
2. Estimate total acres defoliated in all 6 states and log-transform it: xt = log10(Dt) where Dt is area defoliated.
3. Estimate the rate of increase in log-area defoliated (rt = xt+1 - xt.
4. Use the following model for regression analysis:
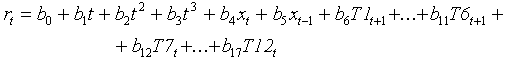
where T1t is January average temperature in year t, T2t is Fanuary average temperature in year t, and so on. Parameters bi should be estimated using regression analysis.
First 3 terms in this equation (after the intercept) are used to filter out the low-frequency trend in the area defoliated. This trend may be related to the spread of gypsy moths, to the change in the area covered by forests, to the change in tree species composition and other non-stationary processes. The next 2 terms represent the autocorrelation in the area defoliated. Finally, the last 12 terms represent temperature effects in 12 months.
In New England, gypsy moths defoliate trees in June. It is logical to expect that any change in areas defoliated from one year to another may be affected by weather conditions in the period from July of one year to June of the next year. Thus, in the model we used the temperature in July - December from year t and the temperature in January - June from year t+1.
5. Excel can analyze maximum 16 independent variables at a time. Thus, you need to do the analysis in several steps. Use first 16 independent variables in regression, then remove those temperature variables that have the smallest effect on the change in defoliation area and add other temperature variables that were skipped in the first analysis. Then again do regression analysis and remove temperature variables that have the smallest effect. Do not remove trend terms even if they are not significant because it is not our objective to analyze the trend. Trend is used only to improve the analysis.
6. At the final step you need to leave only those effects that are significant (except trend effects). Because we considered numerous temperature variables, it is necessary to use Bonferroni correction for the error probability (multiply error probability by 12 which is the number of temperature variables). What is the probability that temperature has no effect on the change in the area defoliated? Don't remove the most significant weather variable even if after Bonferroni correction P > 0.05. Bonferroni correction assumes that all variables are equivalent which in reality is not true. Thus it is necessary to interpret it with caution.
7. Predict the area defoliated in year t+1 from area defoliated in year t and t-1, and weather data. But do not use trend because trend is usually unknown. Replace trend variables by their mean values. Plot predicted and actual values of log area defoliated.