Lab. 5. Model of Leslie

Photo by J.Ogrodnick

The life table of the aphid midge is the following:

Age, days	Stage		Numbers     Eggs laid per female
================================================================
0		egg		1000		 0
1		egg		1000		 0
2		larva		 700		 0
3		larva		 650		 0
4		larva		 600		 0
5		larva		 550		 0
6		larva		 530		 0
7		cocoon		 400		 0
8		cocoon		 400		 0
9		cocoon		 400		 0
10		cocoon		 400		 0
11		cocoon		 400		 0
12		cocoon		 400		 0
13		adult		 350		 5
14		adult		 340		15
15		adult		 330		20
16		adult		 300		20
17		adult		 260		15
18		adult		 200		12
19		adult		 120		 8
20		adult		  40		 5
21		adult		  20		 2
22		adult		   5		 0
================================================================

1. Estimate lx, sx, and mx.

2. Build the matrix of Leslie.

3. Initial age distribution is: 100 midges are in the cocoon stage, and their age is 10 days. To build the model of Leslie use row numbers as age, and column numbers as time. Put the vector of initial distribution into the first column (vertically). The second column is defined using the array equation: Leslie matrix multiplied by the vector in the first column. Use dollar signs when referencing to the Leslie matrix so that you can autofill this equation to the right! To enter a matrix equation do the following:

• Select the second column where the age distribution in the next time step will be estimated.
• Enter the equation, e.g., =MMULT($A$1:$W$23, A31:A53). Here, MMULT is the function for matrix multiplication, $A$1:$W$23 is your Leslie matrix, and A31:A53 is your initial age distribution.
• Press Ctrl+Shift+Enter (on PC) or Apple+Shift+Enter (on Macintosh) to enter the array equation.

4. Run simulation for 200 time steps (autofill the array equation to the right up to the 201-st column).

5. Plot total population numbers vs. time (use both linear and log scale for population numbers).

6. Estimate and plot on one graph the dynamics of eggs, larvae, cocoons and adults (against use both linear and log scales). For log-transformation use LOG(N+1) equation because some numbers = 0.

7. Estimate Ro, T and r from the life table using

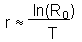
Then estimate r precisely using the equation:

Copy the approximate value of r into a new cell, and then estimate each element in the sum (equation above) using the value of r from that cell. Then estimate the sum and solve the equation using the "Goal Seek" tool. What is the difference between 2 estimates of r? Is the approximate value higher or lower than the precise value?

8. Now estimate r from the results of your simulation. It is equal to the slope of log population numbers vs. time. If you used LOG10 for log-transformation, then you need to multiply the estimated value by ln(10) = 2.3. Estimate this slope using the last 50 time steps (use regression!). Compare this value of r with 2 values obtained in the previous step.

9. Estimate the theoretical age distribution using equation

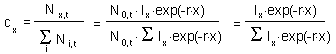
Compare it with the age distribution at the end of your simulation. Does the equation give good prediction? Plot histograms of both age distributions. If the age distribution has not converged close enough to the stable age distribution, then continue simulation for 200 time steps more.