1.2. Models as analytical tools

Population ecology is the most formalized area in biology.
Model is a tool and should never be considered an ultimate goal in ecological studies.
Model and reality are linked together by two procedures: abstraction and interpretation:

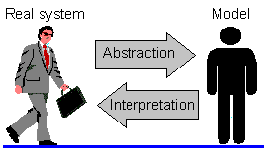
Abstraction means generalization: taking the most important components of real systems and ignoring less important components. Importance is evaluated by the relative effect of system components on its dynamics. For example, if we found that parasitism rate in insect pest is always below 5%, then parasitoids can be excluded from the model.

Interpretation means that model components (parameters, variables) and model behavior can be related to components, characteristics, and behavior of real systems. If model parameters have no interpretation, then they cannot be measured in real systems.

Most field ecologists are not good at abstraction. If they build a model they often try to incorporate every detail. Most mathematicians are not good at interpretation of their models. Usually they think of clean models and dirty reality. However, both abstraction and interpretation are necessary for successful modeling. Thus, close collaboration between ecologists and mathematicians is very important.

Models are always wrong ... but many of them are useful.
How it may happen that the wrong model can give a correct answer? In the same way as old maps, which assumed a flat earth and used wrong distance relations, where useful for travelers in the past.

Modeling strategy:

  1. Select optimal level of complexity
  2. Never plan model development for more than 1 year
  3. Avoid the temptation to incorporate all available information into the model
  4. Follow specific objectives, don't try to make a universal model
  5. If possible, incorporate already existing models
System properties and model properties
  1. Many system properties are not represented in the model.
    Example: age structure is not represented in both exponential and logistic models.
  2. Some model properties cannot be found in real systems.
    Example: solutions of differential equations are always smooth, while trajectories of real systems are always noisy.
Example of a wrong question: Does this population have an equilibrium density?
The stable equilibrium is a state to which all trajectories of the system converge infinitely close with increasing time. The model (e.g. the differential equation) may have an equilibrium density, but real populations don't have it because:
  1. Population density cannot be measured with infinite accuracy.
  2. Weather fluctuations always add noise to system's dynamics.
  3. Time series are never long enough to talk about limits and convergence.

Alexei Sharov 1/12/96