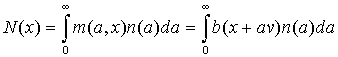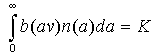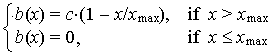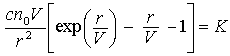Metapopulation model of stratified dispersal
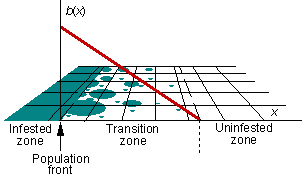
Sharov and Liebhold (1998, Ecol. Appl. 8: 1170-1179. [Get a PDF reprint!]) have developed a metapopulation model of stratified dispersal. This model is based on two functions: colony establishment rate and colony growth rate. The probability of new colony establishment, b(x), decreases with distance from the moving population front, x
Population numbers in a colony, N(a), increases exponentially with colony age, a
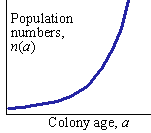 n(a) = noexp(ra)
n(a) = noexp(ra)
where no are initial numbers of individuals in a colony that has just established, and r is the marginal rate of population increase.
The population front is defined as the farthest point where the average density of individuals per unit area, N, reaches the carrying capacity, K:
N = K.
The rate of spread, v, can be determined using the traveling wave equation.
We assume that the velocity of population spread, v, is stationary. Then, the density of colonies per unit area m(a,x) of age a at distance x from the population front is equal to colony establishment rate a time units ago. At that time, the distance from the population front was x + av. Thus, m(a,x) = b(x + av). The average numbers of individuals per unit area at distance x from the population front is equal to:
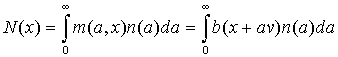 where n(a) is the number of individuals in a colony of age a. The population front is defined by the condition N(0) = K. Thus, the traveling wave equation is
where n(a) is the number of individuals in a colony of age a. The population front is defined by the condition N(0) = K. Thus, the traveling wave equation is
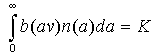
This equation can be used for estimating the rate of population spread. To estimate this integral we need to define explicitly functions b(x) and n(a). We assume a linear function of the rate of colony establishment:
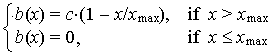 The population of each colony increases exponentially
The population of each colony increases exponentially
n(a) = noexp(ra)
After substituting these functions b(x) and n(a) into the traveling wave equation, we get the following equation
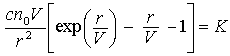
where V = v/xmax is the relative rate of population spread. This equation can be solved numerically for V; and then the rate of spread is estinmated as v = V xmax.
This model can be used to predict how barrier zones (where isolated colonies are detected and eradicated) reduce the rate of population spread. We will assume that the barrier zone is placed in the transition zone at some particular distance from the population front. Because new colonies are eradicated in the barrier zone, we can set the colony establishment rate, b(x), equal to zero within the barrier zone as it is shown in the figure below
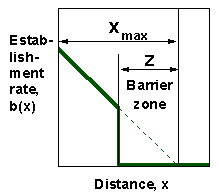
If this new function b(x) is used with the traveling wave equation, we get the rate of spread with the barrier zone. The figure below shows the effect of barrier zone on the rate of population spread. Relative width of the barrier zone is measured as its proportion from the width of the transition zone. Relative reduction of population spread is measured as 1 minus the ratio of population spread rate with the barrier zone to the maximum rate of population spread (without barrier zone).
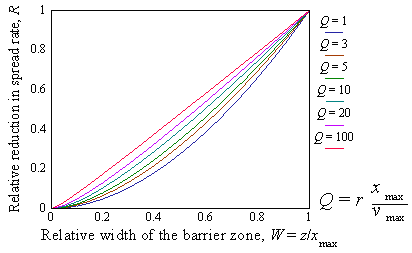
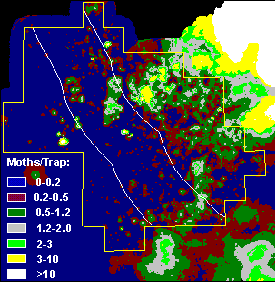
This model predicted that barrier zones used in the Slow-the-Spread project should reduce the rate of gypsy moth spread by 54%. This prediction was close to the 59% reduction in the rate of gypsy moth spread in Central Appalachian Mountains observed since 1990 (when the strategy of eradicating isolated colonied has been started).
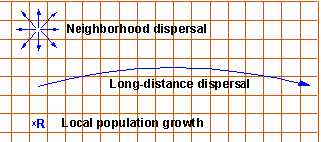
Cellular automata models of stratified dispersal
Cellular automata is a grid of cells (usually in a 2-dimensional space), in which each cell is characterized by a particular state. Dynamics of each cell is defined by transition rules which specify the future state of a cell as a function of its previous state and the state of neighboring cells. Traditional cellular automata considered close neighborhood cells only. However, in ecological applications it is convenient to consider more distant neighborhoods within specified distance from the cell.
|  12.3. Stratified Dispersal
12.3. Stratified Dispersal

 n(a) = noexp(ra)
n(a) = noexp(ra)