2.6. Capture-recapture and Removal Methods

Capture-Recapture Method

Suppose the population is of size N, so that N in the number we wish to estimate. Suppose, M organisms were captured, marked (or tagged) and released back into the population. After some time that should be sufficient for organisms to mix, n organisms were captured, and m of these appeared to be were marked. The proportion of recaptured organisms is assumed to be the same as the proportion of marked organisms:

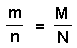
Population size can be found as: N = nM/m (the Lincoln Index).

The following conditions should be met:

  1. No immigration, emigration, births or deaths between the release and recapture times.
  2. The probabilities of being caught are equal for all individuals (including marked ones).
  3. Marks (or tags) are not lost and are always recognizable.
The first two conditions are often non-realistic, and thus, several modifications of this method has been developed that loosen these conditions. Perhaps the most popular is the Jolly-Seber method which requires capturing and marking of animals at regular time intervals. Animals, marked and released each time, should have different marks so that it is possible to distinguish between individuals marked on different dates. Algorithm is given in Southwood (1978).

Jolly-Seber method gives an estimate of population size on each specific date; the first condition can be violated. However, the second condition is still required. It is also possible to estimate mortality+emigration rate and birth+immigration rate on each specific day. These rates are assumed to be constent for all individuals (including marked individuals).

There are numerous other models for capture-recapture experiments, which are specific for a particular population. For example, age structure of the population may be important, or some individuals may have higher probability to be caught than others.

Another problem arises if the population has no boundaries. In this case, a grid of traps can be established, and only the central portion of the grid is used for analysis (because traps near the edges may be influenced by migration). The area covered by the grid should be much larger than the average distance of animal dispersal.

Because the biology of different species is variable, it may be necessary to modify the capture-recapture model.

Removal method

Removal method is based on intensive trapping of animals in an isolated area. Migration is prevented by some kind of barriers. It is assumed that there are no births or natural deaths of organisms. The proportion of animals captured each day is the same. Therefore, population numbers and the number of captured individuals declines exponentially:

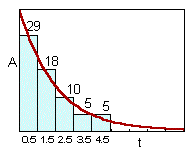
The model of removal: dN/dt = -aN, where a is the removal rate.

The solutionof this differential equation is N = Noexp(-at), where No are initial numbers.

Then the number of animals captured per unit time is equal to A(t) = aNoexp(-at) Parameters a and No can be estimated using the non-linear regression.

Pielou (p. 127) used a different method for estimating parameters which is based on the analysis of 2 first time intervals only. For example, if captures in the first 2 time intervals were 29 and 18 animals, then

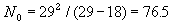
a = (29-18)/29 = 0.38.

This model can be generalized assuming the recruitment of organisms (e.g., emergence of adult insects from the soil).

Alexei Sharov 1/12/96