3.5. Density-Invariant Indexes of Aggregation
Simple indexes of aggregation are specific to a particular population sampled at particular time. They cannot be extrapolated neither in space nor in time, and this is their major limitation. In order to overcome this limitation, several density-invariant indexes has been developed.1. The most frequently used is the "power law" (Taylor 1961):
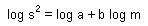
Coefficient b is considered as species-specific. This equation was shown to work well in the wide range of species density. Of course, it is hard to expect that b will be constant in any kind of environment, but for populations in similar environments it is usually stable.
2. Mean crowding regression (Iwao 1968):
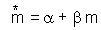
Regression coefficients can be used to distinguish between different patterns of spatial distribution:
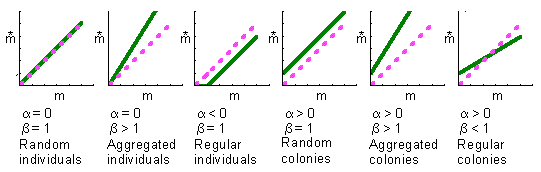
3. Negative binomial k. This is not a good index because usually it is not density-invariant.
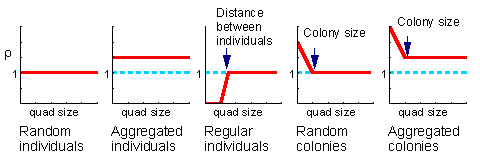
Effect of Quad Size on Aggregation Indexes
Different scales of spatial distribution should be considered. The distribution may be random at small scales and aggregated at larger scales. Thus, it is important to examine the distribution using different quad sizes (quad size = spatial resolution).For example, the distribution is random, if and only if the coefficient of dispersion (CD) is equal to 1 for all the range of quad sizes. Thus, if CD=1 for a specific quad size, then we cannot conclude that the distribution is random, we need to test other quad sizes.
Any index of aggregation can be plotted against quad size. However, there are specialized indexes designed for multiple quad sizes. For example, ro index (Iwao 1972) was defined as:
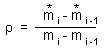
where subscripts 1,2,...i stand for successively increasing sizes of quads. Ro index is used to determine characteristic distances in a spatial distribution: