3.7. Fractal Dimension of Population Distribution
Old definition of a fractal: a figure with self-similarity at all spatial scales.
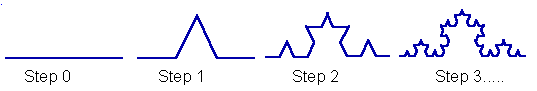
Fractal is what will appear after infinite number of steps.
Examples of fractals were known to mathematicians for a long time, but the notion was formulated by Mandelbrot (1977).
New definition of a fractal: Fractal is a geometric figure with fractional dimension
It is not trivial to count the number of dimensions for a geometric figure. Geometric figure can be defined as an infinite set of points with distances specified for each pair of points. The question is how to count dimensions of such a figure. Hausdorf suggested to count the minimum number of equal spheres (circles in the picture below) that cover the entire figure.
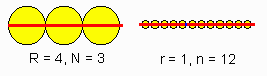
The number of spheres, n, depends on their radius, r, and dimension was defined as:
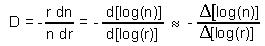
For example, dimension of a line equals to 1 (see figure above):
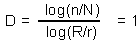
"Normal" geometric figures have integer dimensions: 1 for a line, 2 for a square, 3 for a cube. However, fractals have FRACTIONAL dimensions, as in the example below: Here we use rather large circles, and thus, the precision is not high. For example, we got D=2.01 for a square instead of D=2.
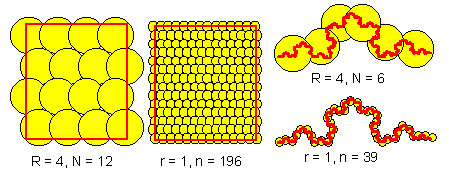
Dimension of a square and fractal is estimated as follows:
Square: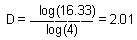 
, Fractal: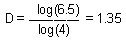
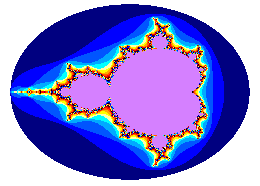
Below is the Mandelbrot set which is also a fractal:
Fractal dimension, D, is related to the slope of the variogram plotted in log-log scale, b:
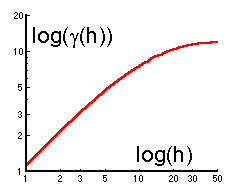
D = 2 - b/2 for a 1-dimensional space
D = 3 - b/2 for a 2-dimensional space
In the figure above, b=1, and thus, D=1.5 for a 1-dimensional space.
