7.5. Modifications of the Leslie model
1. Variable matrix elements. Survival and reproduction rate of organisms may depend on a variety of factors: temperature, habitat characteristics, natural enemies, food, etc. To represent these dependencies, the elements of Leslie model can be replaced by equations that specify survival and reproduction rates as functions of various factors. Equations can be obtained from experimental data.2. Distributed delays. Age and time are equivalent in the original Leslie model, and thus, all organisms develop synchronously with constant rate. However, development rate of invertebrates and plants is not constant: it depends on temperature and may vary among individuals. Individual variation of development rates is called "distributed delay" because there is a distribution of time when organisms reach maturity. Transition matrix can be modified to incorporate these features.
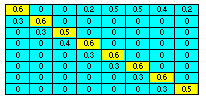 | 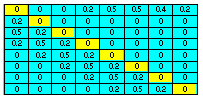 |
| This matrix has non-zero diagonal elements, and thus, some proportion of organisms remain in the same age class when time increases. As a result, development goes slower than it would be in the original Leslie model. The rate of development can be adjusted by changing relative values of diagonal and sub-diagonal elements | This matrix allows organisms to leap over several age intervals in one time step. As a result, development goes faster than it would be in the original Leslie model. The rate of development can be adjusted by changing the length of age leaps. |
3. Partitioning the life cycle into stages. Many invertebrate species have a complex life cycle that includes several stages. For example, holometabolous insects usually have 4 stages: egg, larvae, pupae, and adult. Each of these stages may include several age intervals: In these models, age is no longer measured in calendar time units (e.g., days or years). Instead, it is measured in independent units which can be interpreted as "physiological age". The concept of physiological age will be discussed in details in the next chapter. It can be used to define "rate of development" as the average increment of physiological age per calendar time unit.



