7.4. Estimation of stable age distribution
Equation [5] can be re-written as:
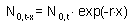
Substituting this equation into [3] we get the relationship between the number of organisms in age x and in age 0 in a stable age distribution:
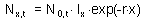
Now we can estimate the proportion of organisms, c , in age x:
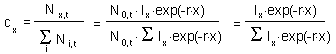 | [7] |
|
Age, x | lx | exp(-rx) | lxexp(-rx) | cx | Simulated cx |
| 0 | 1.000 | 1.0000 | 1.0000 | 0.2413 | 0.2413 |
| 1 | 0.845 | 0.8507 | 0.7188 | 0.1734 | 0.1734 |
| 2 | 0.824 | 0.7237 | 0.5963 | 0.1439 | 0.1439 |
| 3 | 0.795 | 0.6156 | 0.4894 | 0.1181 | 0.1181 |
| 4 | 0.755 | 0.5237 | 0.3954 | 0.0954 | 0.0954 |
| 5 | 0.699 | 0.4455 | 0.3114 | 0.0751 | 0.0751 |
| 6 | 0.626 | 0.3790 | 0.2373 | 0.0572 | 0.0572 |
| 7 | 0.532 | 0.3224 | 0.1715 | 0.0414 | 0.0414 |
| 8 | 0.418 | 0.2743 | 0.1147 | 0.0277 | 0.0277 |
| 9 | 0.289 | 0.2333 | 0.0674 | 0.0163 | 0.0163 |
| 10 | 0.162 | 0.1985 | 0.0322 | 0.0078 | 0.0078 |
| 11 | 0.060 | 0.1689 | 0.0101 | 0.0024 | 0.0024 |
| Total | 4.1445 | 1.0000 | 1.0000 |
Age distribution estimated using equation [7] (column 5) coincided with simulated age distribution after 50 iterations of the model.


