7.3. Estimation of the intrinsic rate of population increase
Previously we discussed an approximate equation:
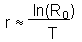
The model of Leslie gives an accurate estimation of r.
Method #1
For simplicity we take years as time units. However, the same logic can be applied to days or weeks.The number of organisms in age x in year t is equal to the number of new-born organisms (x=0) x years ago multiplied by their survival (lx) till age x:
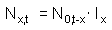 | [3] |
where
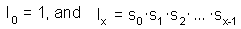
Now, equation [2] of the Leslie model can be re-written as:
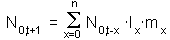 | [4] |
After initial damped fluctuations, the Leslie model shows exponential growth and age distribution stabilizes. Thus, the number of organisms in any age class will grow exponentially. In particular, the number of new-born organisms increases exponentially:
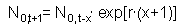
Then,
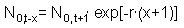 | [5] |
Now we combine equations [4] and [5]:
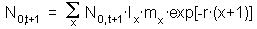
The term N0,t-x can be taken out of the summation expression and then we get the equation:
 | [6] |
Equation [6] can be used to estimate r. The sum at the left side can be estimated for different values of r, and then we can select the r-value that makes this sum equal to 1. It makes sense to start with the r-value estimated using the approximate method discussed in the previous chapter. Thus, we start with r=0.181 and get the sum [6] equal to 0.9033. When r increases, then the value of the sum [6] decreases because r is included as a negative exponent. Obtained value of the sum appeared to be less than 1, and thus, we need to try smaller values of r. Let's select r=0.16. Then the sum is equal to 1.0092. The exact value of r can be found by linear interpolation:
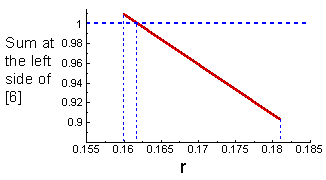
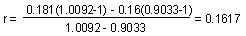
Now we check the solution: when r=0.1617 then the sum [6] is equal to 1.00014 which is very close to 1.
Note: In Pielou (1978), this example is estimated in a different way which is difficult to understand. She constructed a different matrix by adjusting reproduction rates and provided no explanation for this adjustment.
Method #2
Intrinsic rate of population increase can be estimated as the logarithm of the only real and positive eigenvalue of the transition matrix. The theory of eigenvalues is the central topic in linear algebra. It is used to reduce multidimensional problems to one-dimensional problems. I recommend to study this topic for those students who plan to be quantitative ecologists. Here we will only estimate the eigenvalue using available software without going into details of the algorithm. The only real and positive eigenvalue of our matrix is equal to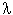
=1.176. Then, r = ln(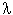) = 0.162 which is very close to the value estimated by method #1.
