9.2. Attractors and Their Types
When the dynamics of a population model is traced over a large number of generations, then the model exhibits an asymptotic behavior which is almost independent from initial conditions (e.g., initial population density). Asymptotic trajectory is called "attractor" because model trajectories converge to this asymptotic trajectory.There may be several attractors in a model. In this case each attractor has a domain of attraction. Model trajectory converges to that attractor in which domain initial conditions were located.
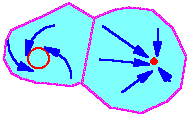
In this example, there are two attractors: a limit cycle (at the left) and a stable equilibrium (at the right). Domains of attraction are colored blue, they never overlap. For different starting places (initial conditions), trajectories converge to different attractors.
Types of attractors:
- Stable equilibrium (=steady state)
- Limit cycle
- Chaos
Examples:



This is a chaotic attractor (Lorenz attractor)


