10.5. Host-Parasitoid Models
Parasitoids are insect species which larvae develop as parasites on other insect species. Parasitoid larvae usually kill its host (some times the host is paralyzed by ovipositing parasitoid female) whereas adult parasitoids are free-living insects (see images of parasitoids). Most of parasitoid species are either wasps or flies.Parasitoids and their hosts often have synchronized life-cycles, e.g., both have one generation per year (monovoltinous). Thus, host-parasite models usually use discrete time steps that correspond to generations (years).
Model of Thompson (1922)
The model assumes that female parasitoids lay their eggs randomly on host individuals and do not distinguish between healthy and already parasitized hosts. In this case, the number of parasitoid eggs laid on one host should have a poisson distribution: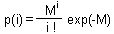
where p(i) is the proportion of hosts that get i parasitoid eggs, and M is the mean number of parasitoid eggs per one host.
Survived hosts are those which get 0 parasitoid eggs. The proportion of survived hosts is equal to p(0) = exp(-M).
Variables:
- P = Density of parasitoid females
- H = Density of hosts
- F = Parasitoid fecundity (no. of eggs laid by 1 female)
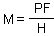 = Average no. of eggs per host individual
= Average no. of eggs per host individual Then, host survival is
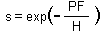
The full model is:
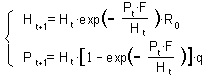
The first equation describes host survival and reproduction. The numbers of survived hosts are multiplied by Ro which means reproduction.
In the second equation, each parasitized host produce one adult parasitoid in the next generation. P is the density of females only. Thus, the numbers of parasitoids is multiplied by the proportion of females = q.
In the model of Thompson, it is assumed that parasites always lay all their eggs. Thus, realized fecundity equals potential fecundity. This assumption implies unlimited search abilities of parasitoids. In nature, parasites often do not realize their potential fecundity just because they can not find enough hosts. Thus, the model of Thompson may overestimate parasitism rates especially if host density is low.
Model of Nicholson and Bailey (1935)
This model is more realistic than the Thompson's model and is widely used by ecologists. It assumes that parasitoid female is able to examine area a ("area of discovery") during its life time. When a host is found, parasitoid lays only one egg in it. However, the same host can be found again later and then the parasite will lay another egg in it because we assume that parasites do not distinguish between healthy hosts and already parasitized hosts.Because each encounter with the host results in depositing 1 egg, the realized fecundity equals the product of the area of discovery and host density: F = aH. Substituting this value of F into the Thompson model we get:
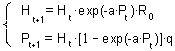
In the Nicholson and Bailey model, the potential fecundity of parasites is not limited. Parasites lay an egg at every encounter with the host even if the number of encounters is very large (e.g., if host density is high). Thus, this model may overestimate parasitism rates at high host density.
Model of Rogers (1972)
The model of Rogers applies the model of Holling, which was originally developed for predator-prey systems, to host- parasite systems. It assumes two kinds of limitations in host-parasitoid interactions: limited parasitoid fecundity (as in the model of Thompson) and limited search rate (as in the model of Nicholson and Bailey).We will use the Holling's disc equation (see section 10.3) to model the functional response of parasitoids. The number of hosts attacked by one parasitoid female is equal to
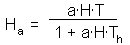
We can modify this equation by setting T=1 because search rate is considered per life time of parasitoid female. Life time can be coded as 1 because the time step is equal to 1 generation. The ratio 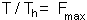 is the maximum fecundity of parasitoid female. Then:
is the maximum fecundity of parasitoid female. Then:
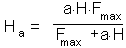
When parasitoid female attacks a host it lays an egg. Thus, realized fecundity F = Ha. Substituting this value of F into the Thompson's model we get:
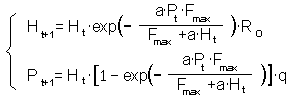
In the model of Rogers, realized fecundity is different from the potential fecundity whereas in previous models this distinction was not present.
All models of host-parasitoid system are unstable: they generate oscillations with increasing amplitude.
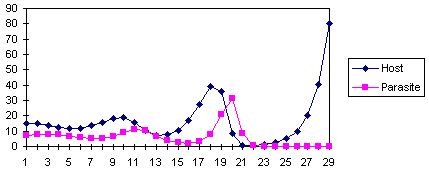
This is the dynamics of the model of Nicholson and Bailey.
However, in nature host-parasitoid population never show oscillations with infinitely increasing amplitude. This is not because the models do not capture the mechanisms of host-parasitoid interactions, but because additional ecological processes (e.g., intraspecific competition in hosts or in parasitoids) can partially or completely stabilize the system. It was also shown that spatial heterogeneity and parasitoid dispersal among host patches may also stabilize the population system.
References:
Nicholson, A. J., and V. A. Bailey. 1935. The balance of animal populations. Proceedings of the Zool. Soc. of London. 1: 551-598.Rogers, D. J. 1972. Random search and insect population models. J. Animal Ecol. 41: 369-383.
Thompson, W. R. 1929. On the relative value of parasites and predators in the biological control of insect pests. Bull. Entomol. Res. 19: 343-350.


