11.2. Competition between Species

Major problems:

1. In conservation ecology: to prevent extinction of particular species; predict potential losses in species composition after introduction of competitors; to reduce competition effects.
2. In biocontrol: to find an exotic natural enemy which will successfully fit into the community of existent natural enemies; to find exotic non-pest competitors that may oust the pest species.

Now, we will introduce the second (competing) species. As a result, the figure becomes two-dimensional:

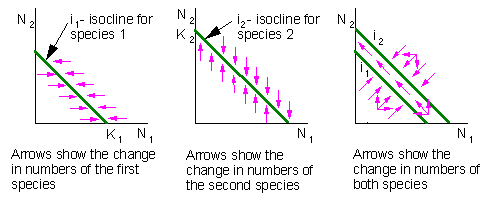
In this example, species #1 becomes extinct as a result of its competition with species #2.

Competitive exclusion principle was first formulated by Grinnell (1904) who wrote:

"Two species of approximately the same food habits are not likely to remain long evenly balanced in numbers in the same region. One will crowd out the other; the one longest exposed to local conditions, and hence best fitted, though ever so slightly, will survive, to the exclusion of any less favored would-be invader."

If competing species are ecologically identical (use the same resource), then inter-specific competition is equivalent to intra-specific competition. Each organism competes with all organisms of both populations. As a result, population growth rate of each population is determined by the sum of numbers of both populations:

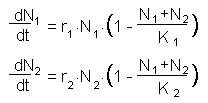
Excel spreadsheet "lotkcomp.xls"

In this case, both isoclines are parallel and have a slope of 45° (see figures above). The species that have a higher carrying capacity (K) always wins. Higher carrying capacity means that the species can endure more crowding than the other species (e.g., due to more effective search for resources). Competitive exclusion is called K-selection because it always go in the direction of increasing K.

If competing species are sufficiently different then intra-specific competition is stronger than inter-specific competition. Organisms of another species are not considered as "full" competitors. As a result, the numbers of inter-specific competitors is multiplied by a weight wi<1:

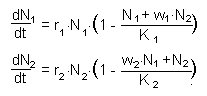
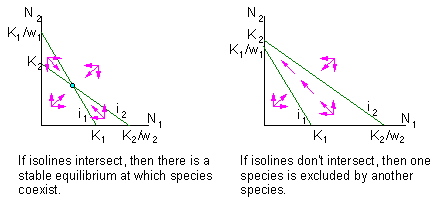
Theoretically it is possible that weights wi>1. This means that organisms of another species are stronger competitors than organisms in the same population. I don't know any example of this sort. But this situation is always discussed in ecological textbooks. If wi>1 and isoclines intersect, then one species will oust the second one, but what species will be excluded depends on initial conditions (initial numbers of both populations):

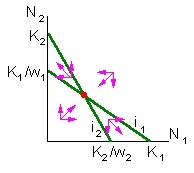
This system has an unstable equilibrium which separates 2 areas of attraction: (1) where the first species ousts the second one and (2) where the second species ousts the first one.

Excel spreadsheet "compet.xls"

Thus, species coexistence is possible if intraspecific competition is stronger than interspecific competition. This occurs if competing species have different preferences in resource usage.

When the principle of competitive exclusion became widely known among ecologists, it seemed to contradict with some well known facts and this contradiction was formulated as "paradoxes". For example, "plankton paradox" focused on the variability of plankton organisms which all seemed to use the same resources. All plankton algae use solar energy and minerals dissolved in the water. There are not so many mineral components as compared to a large variability in plankton algae species.

There is no final solution for this paradox. However, it became clear that coexistence of species that use the same resource is a common phenomenon. Mathematical models described above are correct, but they are oversimplified; thus it is difficult to apply them to real species. More complicated and more realistic models indicate that species coexistence is possible. For example, plankton algae have distinct seasonality in their abundance which is ignored in the simple Lotka-Volterra model. Cyclical dynamic regime allows species to coexist even if they cannot coexist in stable systems. Another important factor is spatial heterogeneity which effect is substantial even in such homogeneous systems as the ocean.